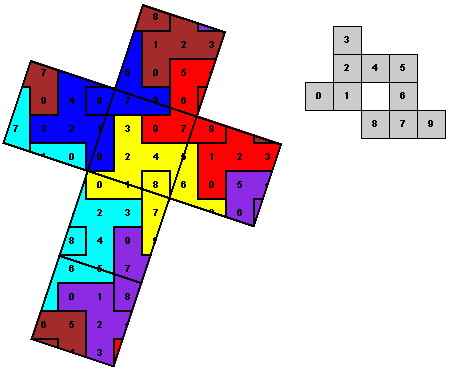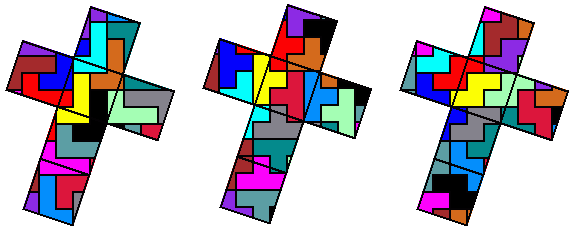
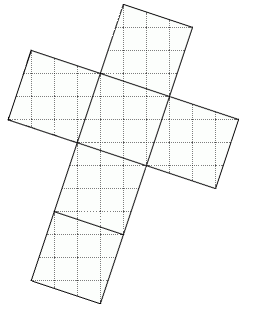
Wie ooit op het idee gekomen is om het oppervlak van een kubus te bedekken met polyomino's, ik weet het niet. Maar de materie is boeiend genoeg om er een pagina aan te besteden. Laten we beginnen met 60 eenheidsvierkantjes. Een vlak van de kubus moet dan 60 : 6 = 10 vierkantjes hebben, hetgeen betekent dat de lengte van de ribbe gelijk is aan √10. Volgens Pythagoras kan die lengte verkregen worden met √(32 + 12). In de nevenstaande tekening ziet u een platgeslagen kubus met de eenheidsvierkanten.
Volgens kenners zijn er miljarden oplossingen mogelijk met de twaalf verschillende pentomino's. Het wordt interessanter als we de kubus gaan bedekken met congruente polyomino's, bijvoorbeeld met 15 tetromino's:
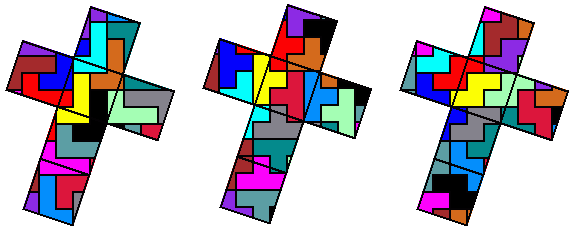
Merkwaardig is dat er voor de andere twee tetromino's geen oplossingen mogelijk zijn.
De drie vierkantjes die een hoekpunt van de kubus raken onderscheiden zich van de overige: zij worden omringd door zeven buren, terwijl alle andere er acht hebben. Om die reden kan de vierkante tetromino nooit drie hoekvakjes bevatten, hij komt dan met zichzelf in de knoop.
Bij de pentomino's heeft alleen de U-pentomino geen oplossing, alle andere wel:
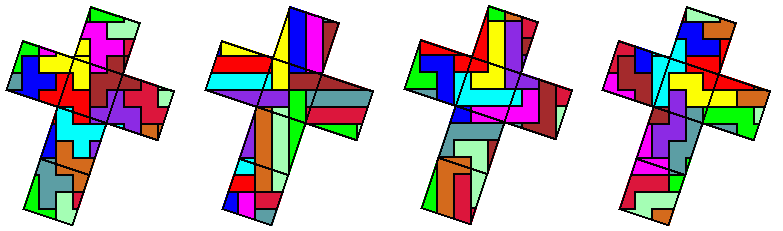
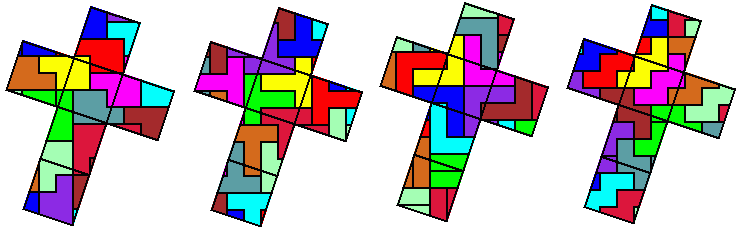
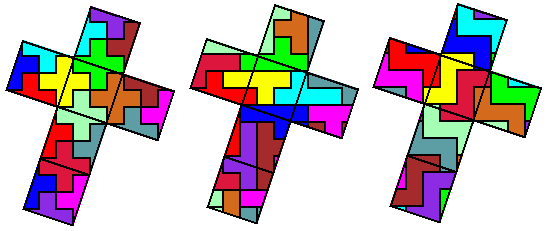
Ook met hexomino's kan de kubus beplakt worden, ik geef er vier van de 16 mogelijke, de andere 19 hebben geen oplossing.
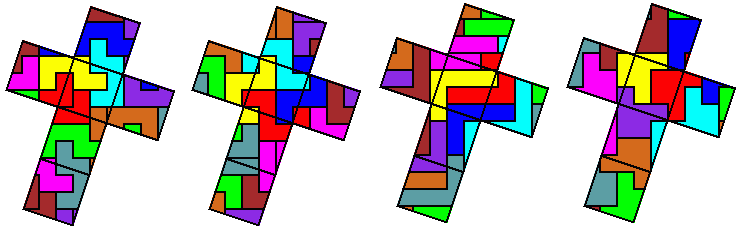
Tot slot een bijzondere dekomino: deze heeft een gat, maar toch is er een oplossing mogelijk omdat het gat zich om de hoek vouwt. Er zijn acht hoeken beschikbaar, voldoende voor zes gaten. Voor 156 van de 4655 dekomino's zijn oplossingen mogelijk.
