Polyomino's

In 1953 introduceerde Solomon W. Golomb, toen student aan de Harvard Universiteit, de term polyomino voor figuren die gevormd worden door eenheidsvierkanten samen te voegen. Omdat een domino bestaat uit twee aaneengesloten vierkanten, stelde Golomb voor figuren met drie vierkanten tromino's te noemen. Die met vier vierkanten tetromino's. En verder pentomino's, hexomino's, heptomino's enz.

De eenheidsvierkanten kunnen op verschillende manieren aaneengesmeed worden. Er is één monomino en één domino. Er zijn twee verschillende tromino's, vijf verschillende tetromino's en twaalf verschillende pentomino's:

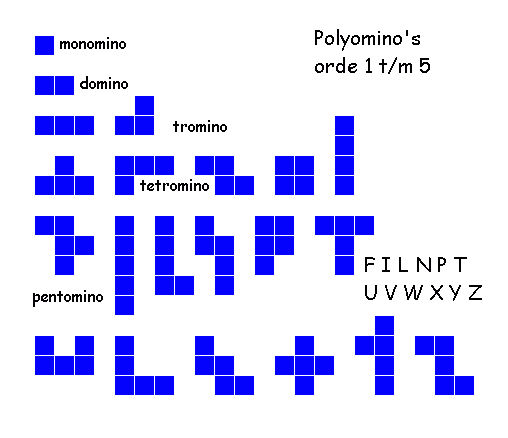
Vooral de pentomino's zijn populair geworden, hetgeen vooral te danken is aan hun aantal. De 12 pentomino's bestaan samen uit 12 x 5 = 60 eenheden, het getal 60 heeft vele delers. Men kan rechthoeken vormen van 3x20, 4x15, 5x12 en 6x10. Ook een schaakbord kan men vullen door 4 vakjes niet te gebruiken. Zie onderstaande voorbeelden:

Als men van vierkanten kubussen maakt kan men zelfs een driedimensionale ruimte van 3x4x5 vullen, er zijn 3940 verschillende oplossingen.

Een oud probleem is het volgende: vul een schaakbord waarvan twee hoekvakjes ontbreken, met 31 domino's. Dat is niet mogelijk, vanwege het feit dat het aantal witte vakjes ongelijk is aan het aantal zwarte vakjes. En hoe je een domino ook neerlegt, hij zal altijd een wit en een zwart vakje bezetten. Iets dergelijks doet zich voor bij hexomino's: er zijn 24 figuren met 3 witte en 3 zwarte eenheden, en 11 figuren met 2 witte en 4 zwarte (andersom mag ook). Omdat 11 oneven is, is het verschil tussen het aantal witte en zwarte vakjes ten minste 2. Het maximale verschil is 2 x 11 = 22.  Een rechthoek kan dus niet gevormd worden met hexomino's, omdat het verschil tussen de aantallen witte en zwarte vakjes in een rechthoek altijd 1, 0 of -1 is.

Hieronder staan wat zelf bedachte voorbeelden.

Met een set pentomino's kan een kerstboompje gemaakt worden, zie het voorbeeld hiernaast. Er zit een lelijk punt in deze oplossing: vier pentomino's raken elkaar. De opgave luidt: vind een oplossing met dezelfde figuur waarbij dit niet het geval is. Er is slechts één oplossing mogelijk (de gespiegelde laten we buiten beschouwing).
Hexomino's worden gevormd met zes vierkantjes; er zijn er 35; een getrapte vorm ziet u hiernaast.
Met 36 hexomino's (men neme een willekeurige erbij) zou men zes keer een rechthoek van 6 bij 6 eenheden kunnen maken. Het is niet bewezen dat dat onmogelijk is, maar verschillende mensen hebben met behulp van een computer aangetoond dat er geen oplossing is. Wel is het mogelijk de zes rechthoeken te maken met 35 hexomino's en twee tromino's.
Er zijn 108 heptomino's, waarvan een met een gat. In nevenstaande figuur staat deze keurig in het midden.
Pentakubussen zijn drie-dimensionale pentomino's; er zijn er 29, die hiernaast samen een fraai bakje vormen.
Als men de 17 niet-platte pentakubussen op tafel legt met zo veel mogelijk eenheden in het grondvlak, hoeveel eenheden maken dan maximaal contact met de tafel? Dat zijn er 65. In de nevenstaande figuur van 5 bij 13 liggen die 65 eenheden in de eerste laag, terwijl de overige 20 een stylistische '8' vormen. Voor deze figuur is slechts één oplossing mogelijk!
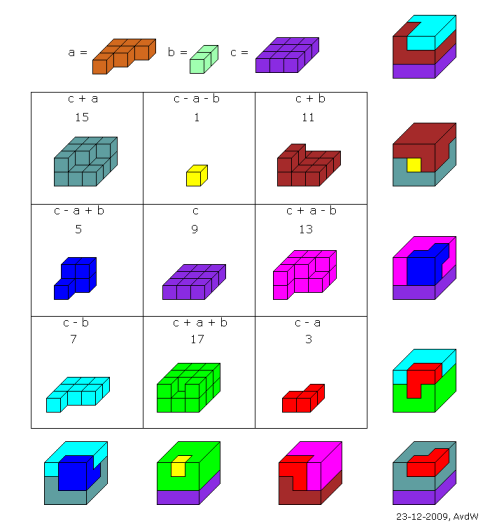
In de geomagie kunnen polykubussen ook een rol spelen. In nevenstaande figuur staan in een magisch vierkant van orde 3 negen polykubussen met aantal kubussen 1, 3, 5, ... 13, 15, 17. De magische som is 27, dat aantal is precies de inhoud van een 3x3x3-kubus. Geomagie is uitgevonden door Lee Sallows, de man van de zelfverwijzende zinnen. Hij schreef: This marvellous 3D 3×3 square with cubical target was produced by Aad van de Wetering of Drieburgen (sic), a recognized name in recreational math circles in Holland. Note that piece sizes form the consecutive series of odd numbers 1,3,5,.., while the piece shapes reflect a textbook application of Lucas's formula, shown alongside. In deze pdf staan er nog meer.

De twaalf vergrote pentomino's bestaan uit negen verschillende pentomino's, maar nooit hun evenbeeld.
Er zijn negen sets van twaalf pentomino's gebruikt. Er zijn 69.153 oplossingen mogelijk.

Wie het programma wil hebben voor het vullen van willekeurige ruimtes met polyomino's kan dat laden op deze pagina.

Zie ook de spoorpentomino's, waar pentomino's een gesloten circuit vormen.
Ook spoorhexomino's zijn mogelijk, met dank aan Edo Timmermans.
Zie voorts lange smalle paden en lange knippen.
Hoeveel symmetrische pentominotrio's zijn er?

Zie ook de polyamonds, die in plaats van vierkanten gelijkzijdige driehoeken als basiseenheid hebben.
Zie ook de polyhexes, die in plaats van vierkanten gelijkzijdige zeshoeken als basiseenheid hebben.

Een prachtige weblocatie over polyvormen is die van Andrew L. Clarke.
Bij pentominoproject T.I.D.Ronse kunt u zien wat allemaal met pentomino's mogelijk is.

Startpagina